• Généralités sur les Eurocodes
  • Les Eurocodes
  • L'Eurocode 2
  • Différences EC2/BAEL
• Actions et combinaisons
  • Notion d'état limite
  • Combinaison ELS
  • Combinaison ELU
  • Actions permanentes
  • Actions variables
• Matériaux
  • Généralités
  • Notion de loi de comportement
  • Comportement du béton
  • Modélisation du béton
  • Comportement de l'acier
  • Modélisation de l'acier
  • Fatigue
    • A1.7.1
    • A1.7.2
    • A1.7.3
• Valeurs caractéristiques
  • limites de calcul
  • limites de l'acier
  • notion de pivot
• Ouvrages et environnement
  • Classification structurale
  • Classes d'exposition
  • Enrobage
• Analyse structurale
  • Généralités
  • liaisons
  • méthode élastique linéaire
  • Géométrie
  • chaînages
• Flexion
  • FS: dimensionnement ELS
  • FS: dimensionnement ELU
  • Flexion déviée
  • règles technologiques
• Cisaillement
  • Généralités
  • Ame
  • Ame-membrure
• Poteaux-voiles
  • généralités
  • conditions géométriques
  • règles technologiques : poteaux
  • règles technologiques : voiles
• Eléments horizontaux
  • arrêt de barres
• Eléments particuliers
  • fondations superficielles

Accueil/Cours/Poteaux-voiles /méthode simplifiée

METHODES SIMPLIFIEES ET REGLES PROFESSIONNELLES

 

1 Poteaux isolés

C’est un critère qui est basé sur le calcul de l’élancement λ défini par :

λ= l₀/i

où :
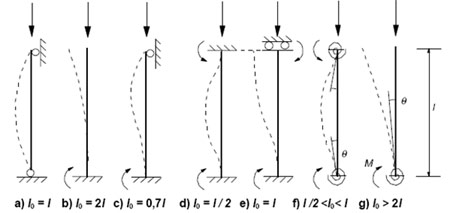
• l₀ est la longueur efficace (ou de flambement) déduite des longueurs réelles des éléments isolés (cf. figure 4).
• i est le rayon de giration de la section de béton non fissurée (`i= sqrt(l/A)` , avec I moment d’inertie et A aire de la section droite. Pour une section rectangulaire (b*h), `i=h/(sqrt(12))`

Figure 1 : Exemples de modes de flambement et longueurs efficaces correspondantes dans le cas d’éléments isolés

Les cas f et g de la figure 1 concernent les éléments comprimés des ossatures. Dans ce cas la longueur l₀ dépend de la souplesse relative des liaisons d’extrémité :

Eléments contreventés (fig.1f) (le nœud supérieur ne peut pas  se déplacer par rapport au nœud inférieur)	`l_0=0.5l sqrt((1+k_1/(0.45+k_1)) (1+ k_2/(0.45+k_2))`
Eléments non contreventés (fig.1g) (le nœud supérieur peut se déplacer par rapport au nœud inférieur)	`l_0 = l max [sqrt(1+10(k_1k_2)/(k_1+k_2) ; (1+k_1/(1+k_1)) (1+k_2/(1+k_2))]]`

Tableau 1. Longueur de flambement des éléments comprimés des ossatures

avec `k= (EITheta)/(ML)` où EI est la rigidité en flexion de l’élément considéré, θ la rotation définie sur la figure 4 et L la hauteur libre entre les liaisons d’extrémité.
A titre d’exemple, pour une poutre isostatique sur appuis simples, on a M = 3EIθ/l ce qui correspond à une rigidité de liaison k = 1/3.

Remarques
• Pour un encastrement parfait, on a k = 0 et pour une extrémité libre k = ∞. Les cas idéaux d’encastrement parfait n’existant pas, la valeur minimale adoptée pour k₁ et k₂ est 0,1.
• Si un élément comprimé au-dessus ou au-dessous d’un nœud est susceptible de contribuer à la rotation lors du flambement, EI/L est remplacé par [(EI/L)_a + (EI/L)_b] où a et b se rapportent aux deux éléments comprimés situés de part et d’autre du nœud.
• Les longueurs efficaces définies le sont pour des sections non fissurées à l’ELU.
• Pour les éléments de section et/ou d’effort normal variables, le calcul de l₀ est basée sur l’estimation de la charge de flambement N_B par : l₀ = `pi sqrt((El)/(N_B))`
• Pour les voiles, le calcul de la longueur efficace inclut un coefficient ß qui dépend des conditions d’appuis, article [12.6.5.1] de l’EC2.

Ayant défini les paramètres permettant de calculer l’élancement λ, on peut alors décliner le critère simplifié d’élancement :

On admet que les effets du 2e ordre peuvent être négligés si l’on a λ≤λlim.

L’EC2 recommande de prendre (valeur reprise dans l’annexe nationale)

λ_lim=20.A.B.C / `sqrt(n)`

où :
• A = `1/(1+0.2φ_(ef))`   (φ_ef est le coefficient de fluage effectif défini dans la prise en compte des effets du fluage).
• B = `sqrt(1+2omega)`  (ω est le ratio mécanique d’armatures, `omega` = `(A_(s)f_(yd))/(A_cf_(cd))`  , A_s aire totale des armatures, f_yd limite élastique de calcul de l’acier, f_cd valeur de calcul de la résistance en compression du béton, A_c aire de la section droite de béton (article [1.6] de l’EC2)).
• C = 1.7-r_m (rm est le rapport `M_(01)/M_(02)`  des moments du 1^er ordre aux extrémités avec |M₀₁|≥|M₀₂|).
• n= `N_(ed)/(A_cf_(cd))`  est l’effort normal relatif

Remarques
• Lorsque les différents paramètres définis ci-dessus ne sont pas connus, on peut adopter comme valeurs par défaut, les valeurs forfaitaires : A = 0.7, B = 1,1 et C = 0,7 et on aura alors λ_lim = 10.78 `1/sqrt(n)`  .
• Si les moments aux extrémités M₀₁ et M₀₂ engendrent de la traction du même côté, r_m est considéré comme positif (C ≤ 1.7) et négatif dans le cas contraire (C ≥ 1.7).
• r_m doit être pris égal à 1 (C = 0.7) dans le cas d’éléments contreventés soumis à des moments du 1^er ordre dus uniquement ou de façon prédominante à des imperfections ou à un chargement transversal, ou dans le cas d’éléments non contreventés.
• Dans le cas de la flexion déviée, le critère d’élancement est vérifié dans les deux directions et l’on pourra négliger les effets du 2^e ordre dans les deux directions, dans aucune direction ou dans une seule des deux directions.

2 Poteaux non isolés

On peut négliger les effets du 2e ordre dans les bâtiments lorsque :

`F_(v,Ed)<= k_1 n_s/(n_s+1.6) (sumE_(cd) l_c)/L^2`

où :
• F_V,Ed est la charge verticale totale sur tous les éléments (contreventés et NON contreventés).
• n_s est le nombre d’étage.
• L est la hauteur totale du bâtiment.
• E_cd est la valeur de calcul du module d’élasticité du béton, `E_(cd) = E_(cm)/gamma_(cE)` défini dans la description de la méthode générale (Y_CE = 1,2)
• I_c est le moment d’inertie de la section béton non fissurée des éléments de contreventement.
• k₁ est recommandée dans l’EC2 (valeur reprise dans l’annexe nationale) et vaut k1 = 0.31. Cette valeur peut être remplacée par k₂ = 0.62 si l’on peut montrer que les éléments de contreventement sont non fissurés à l’ELU.

Par ailleurs, l’expression n’est valable que si l’on a en plus les conditions suivantes qui sont toutes remplies :

• L’instabilité de torsion est négligeable (structure raisonnablement symétrique).
• Les déformations globales d’effort tranchant sont négligeables (cas des voiles de contreventement sans grandes ouvertures).
• Les rotations en pied des éléments de contreventement sont négligeables.
• La rigidité des éléments de contreventement est sensiblement constante sur la hauteur.
• La charge verticale totale augmente approximativement de la même quantité à chaque étage.

3 Dimensionnement lorsque les effets du second ordre sont négligés

4 Dimensionnement selon les règles professionnelles

La méthode de calcul des aciers, conforme à la méthode historique du BAEL peut être utilisées dans la mesure où….(à faire)