NOTION DE LOI DE COMPORTEMENT
1 Cas du béton
Réponse en compression
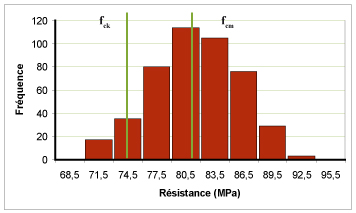
La résistance en compression du béton est définie, conformément à l'approche statistique de la norme NF EN 206-1, comme le fractile1 5% de la distribution des résistances. En effet, le béton étant fabriqué avec des matériaux hétérogènes qui peuvent varier sur la durée d'un chantier et qui sont mis en œuvre dans des conditions variables (température, hygrométrie mais aussi conditions de chantier), sa résistance peut varier au cours d'un chantier. La figure 1 montre par exemple l'histogramme des résistances mesurées lors du chantier du pont de Normandie. Dans cet exemple la moyenne des résistances mesurées fcm est égale à 81,6 MPa et l'écart type s est égal à 4,5 MPa. Si l'on considère que la distribution des résistances suit une loi normale, le fractile 5% fck est égal à
fcm – 1,645 s (soit 74,2 MPa dans l'exemple de la figure 1). L'Eurocode Béton adopte, pour simplifier, la relation suivante :
fcm = fck + 8 MPa
ce qui correspond à un écart-type voisin de 5 MPa. On notera que cette relation indique que le coefficient de variation (rapport entre s et fcm) diminue avec la résistance. La dispersion n'est donc pas plus grande avec des bétons hautes performances qu'avec des bétons courants.
|
|
|
Figure 1 : distribution des résistances des bétons du viaduc d'accès Nord du pont de Normandie |
Mesure de la résistance en compression
La résistance caractéristique du béton est obtenue à partir d'essais de compression à 28 jours après le coulage du béton sur des éprouvettes cylindriques d'élancement (rapport hauteur/diamètre) égal à 2. En France on utilise couramment un cylindre de diamètre voisin de 16 cm (en fait tel que la section soit égale à 200 cm2) et de hauteur 32 cm. Mais la norme NF EN 206-1 autorise l'emploi d'éprouvettes cubiques utilisés dans d'autres pays comme l'Allemagne et le Royaume-Uni. C'est pourquoi la classe d'un béton s'exprime par exemple par C 30/37 (béton de résistance 30 MPa sur cylindre ou 37 sur cube).
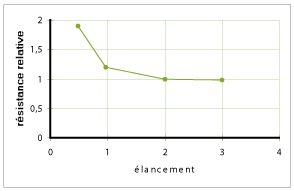
L'avantage des éprouvettes cubiques vient du fait que les faces de chargement sont directement obtenues en faisant faire un quart de tour à l'éprouvette sortie du moule alors que pour un cylindre on doit surfacer les faces d'appui. Toutefois, un élancement égal à un a pour conséquence que l'influence des conditions aux limites se fait sentir dans tout le volume (c'est le frettage : le contact béton-presse est frottant et gêne la déformation latérale du béton). Cela conduit à surestimer la résistance (cf. figure 2) : on constate qu'avec un cube on surestime d'environ 20% la résistance obtenue sur cylindre Aussi la norme NF EN 206-1 prévoit une correspondance entre la résistance sur cube et sur cylindre (tableau 1).
|
|
|
Figure 2 : évolution de la résistance en compression avec l'élancement; éprouvette cylindrique. La résistance relative est calculée en divisant la résistance par celle obtenue avec un élancement égal à 2 [Hansen, 62]. |
| fck (MPa) |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
fck,cube (MPa) |
25 |
37 |
50 |
60 |
75 |
85 |
95 |
105 |
Tableau 2 : extrait du tableau 3.1 de l'EC2 – relation entre fck et fck,cube .
Le frettage explique aussi la formation de cônes de rupture sous les appuis de chargement (figure 3).
a)  |
b) |
|
Figure 3 : a) éprouvette Φ 16 H32 après un essai de compression ; le faciès de rupture "en cône" est dû au phénomène de frettage |
Figure 3 : b) cube d'arête 15 cm après un essai de compression ; le frettage affecte dans ce cas tout le volume. |
Resistance en traction
mesure de la résistance à la traction
Cette résistance est déterminée à partir de trois types d’essais : traction directe, traction par flexion, traction par fendage.
fctm correspond à la résistance en traction directe (traction uni-axiale centrée). Très souvent la résistance en traction est estimée par un essai de traction par fendage (essai dit brésilien – cf. figure 8 et film de l'essai). Dans ce cas la résistance en traction fct peut être estimée à partir de celle mesurée fct,sp par la relation fct = 0,9 fct,sp. Le fait que la résistance en traction par fendage soit plus élevée que la résistance en traction directe s'explique par un effet d'échelle : dans l'essai de fendage le plan de rupture est imposé par l'essai, alors que dans l'essai de traction directe c'est le plan le plus faible qui va se rompre. Il y a donc plus de chance d'avoir un plan plus faible dans ce dernier essai.
On notera enfin que l'Eurocode Béton définit pour la résistance en traction avec deux fractiles :
5% (fctk, 0,05 = 0,7 fctm) et 95% (fctk, 0,95 = 1,3 fctm). En effet, selon les applications on se placera du coté de la sécurité en prenant l'un ou l'autre des fractiles.
La résistance à la traction est souvent calculée à partir de la résistance à la compression. L’EC2 propose une relation (lien vers A1.5).
2 Cas de l'aciers
L'Eurocode béton (EC2) s'applique aux aciers à haute adhérence de limite élastique caractéristique (voir la notion de grandeur caractéristique ) allant de 400 MPa à 600 MPa. En France, la limite élastique couramment rencontrée est celle des aciers haute adhérence (HA) et elle est égale à 500 MPa avec un fractile de 5%. On notera que l'EC2 ne fait plus référence aux aciers lisses, ni à des aciers de limite élastique inférieure à 400 MPa (acier doux dont la limite élastique caractéristique est égale à 235 MPa). Ces aciers ne peuvent pas être pris en compte dans le dimensionnement. Ils ne sont donc pratiquement plus utilisés en béton armé sauf dans des cas très spécifiques : lorsque de nombreux pliages dépliages sont à prévoir et pour les crochets de levage d’éléments préfabriqués ou des ancrages de platine métalliques.
Les aciers de béton armé sont livrés sous forme d'armatures ou de treillis composés d'armatures soudées. La norme NF EN 10080 consacrée aux aciers soudables pour béton armé (barres, couronnes, treillis soudés et treillis raidisseurs) définit la manière de mesurer l'adhérence (essais beam test et pull-out test) et donne le tableau des diamètres nominaux préférentiels, des sections et masses linéiques nominales.
Compte tenu des verrous et empreintes, la section des armatures à haute adhérence n'est pas tout à fait circulaire. Le diamètre nominal correspond donc à celui du cercle ayant la même section que l'armature.
Tableau des diamètres nominaux préférentiels, des sections et masses linéiques nominales (repris de NF EN 10020).
|
Diamètre nominal mm |
Barres |
Treillis soudés |
Section nominale mm2 |
Masse linéique nominal kg/m |
|
5 |
|
X |
19,6 |
0,154 |
|
5,5 |
|
X |
23,8 |
0,187 |
|
6 |
X |
X |
28,3 |
0,222 |
|
6,5 |
|
X |
33,2 |
0,260 |
|
7 |
|
X |
38,5 |
0,302 |
|
7,5 |
|
X |
44,2 |
0,347 |
|
8 |
X |
X |
50,3 |
0,395 |
|
8,5 |
|
X |
56,7 |
0,445 |
|
9 |
|
X |
63,6 |
0,499 |
|
9,5 |
|
X |
70,9 |
0,556 |
|
10 |
X |
X |
78,5 |
0,617 |
|
11 |
X |
X |
95 |
0,746 |
|
12 |
X |
X |
113 |
0,888 |
|
14 |
X |
X |
154 |
1,21 |
|
16 |
X |
X |
201 |
1,58 |
|
20 |
X |
|
314 |
2,47 |
|
25 |
X |
|
491 |
3,85 |
|
28 |
X |
|
616 |
4,83 |
|
32 |
X |
|
804 |
6,31 |
|
40 |
X |
|
1257 |
9,86 |
|
50 |
X |
|
1963 |
15,4 |
1Le fractile 5% d'une distribution (ensemble de valeurs d'un paramètre comme la résistance) signifie que 5% des valeurs de la distribution sont inférieures à ce fractile (ou bien 95% des valeurs sont plus fortes.