• Généralités sur les Eurocodes
  • Les Eurocodes
  • L'Eurocode 2
  • Différences EC2/BAEL
• Actions et combinaisons
  • Notion d'état limite
  • Combinaison ELS
  • Combinaison ELU
  • Actions permanentes
  • Actions variables
• Matériaux
  • Généralités
  • Notion de loi de comportement
  • Comportement du béton
  • Modélisation du béton
  • Comportement de l'acier
  • Modélisation de l'acier
  • Fatigue
    • A1.7.1
    • A1.7.2
    • A1.7.3
• Valeurs caractéristiques
  • limites de calcul
  • limites de l'acier
  • notion de pivot
• Ouvrages et environnement
  • Classification structurale
  • Classes d'exposition
  • Enrobage
• Analyse structurale
  • Généralités
  • liaisons
  • méthode élastique linéaire
  • Géométrie
  • chaînages
• Flexion
  • FS: dimensionnement ELS
  • FS: dimensionnement ELU
  • Flexion déviée
  • règles technologiques
• Cisaillement
  • Généralités
  • Ame
  • Ame-membrure
• Poteaux-voiles
  • généralités
  • conditions géométriques
  • règles technologiques : poteaux
  • règles technologiques : voiles
• Eléments horizontaux
  • arrêt de barres
• Eléments particuliers
  • fondations superficielles

• Bloc outils
  • Textes de référence
    • Références

Accueil/Cours/Poteaux-voiles /conditions géométriques

GEOMETRIE ET BASES DE CALCUL

1 Notion d’élément isolé

Dans l’EC2, la distinction est faite entre éléments isolés et structures, les critères permettant de s’affranchir des effets du 2è ordre étant différents. Pour cela il convient donc de définir ce qu’est :
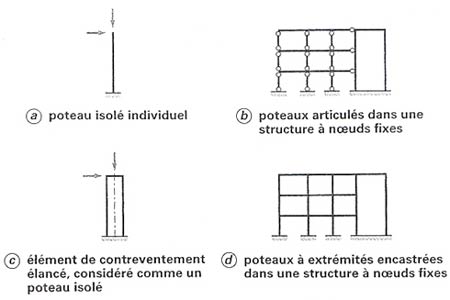
Un élément isolé : c’est un élément effectivement isolé ou que l’on peut considérer structurellement comme isolé (cf. figure 1).
 

Figure 1 : Types d’éléments comprimés isolés (d’après [3])

Deux paramètres sont importants lorsque l’on est amené à considérer les effets du 2^e ordre :
• La longueur de flambement ou longueur efficace (l₀ ou l_f) qui fait intervenir les conditions de liaison du poteau.
• La charge critique de flambement (ou charge d’Euler NB) obtenue à partir de la relation moment –courbure de la théorie des poutres et qui vaut NB =  `(pi^2El)/(l_(f^2)`

Si l’élément n’est pas isolé, les poteaux se retrouvent au sein d’une structure (planchers, voiles ou portiques à nœuds déplaçables ou non).

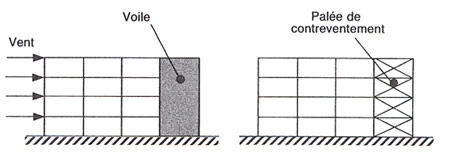
Figure 2 : Portiques à nœuds non déplaçables (d’après [5])

 

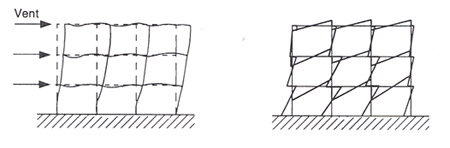
Figure 3 : Portiques à nœuds déplaçables (d’après [5])

 
Eléments ou systèmes contreventés : éléments ou sous-ensembles structuraux dont on admet pour l’analyse et le dimensionnement qu'ils ne contribuent pas à la stabilité horizontale de l'ensemble.
Eléments ou systèmes de contreventement : éléments ou sous-ensembles structuraux dont on admet pour l’analyse et le dimensionnement qu’ils contribuent à la stabilité horizontale de l’ensemble.

Dans le cas le plus général, la prise en compte des effets du 2e ordre peut être négligée si ces derniers n’atteignent pas 10% des effets du 1er ordre correspondants.

Il est souvent assez difficile d’estimer correctement la contribution relative de ces différents effets. Ainsi, des critères simplifiés permettent de s’affranchir des effets du 2^e ordre sous certaines conditions.

2 Imperfections géométriques des éléments de la structure

Aux états limites ultimes, l’analyse des éléments et des structures doit tenir compte des effets défavorables des imperfections géométriques éventuelles de la structure ainsi que des écarts dans la position des charges.

Les imperfections peuvent être représentées par une inclinaison θi :

θ_i = θ₀.α_h.α_m

où  θ₀ est la valeur de base : θ₀ = 1/200
     α_h est un coefficient de réduction relatif à la longueur ou la hauteur : α_h = 2/l^0,5
     α_m est un coefficient de réduction relatif au nombre d’éléments : α_m = [0,5(1+1/m)]^0,5
     l est une longueur ou une hauteur exprimée en mètres
     m est le nombre d’éléments verticaux contribuant à l’effet total

Élément non contreventé                                   Élément contreventé

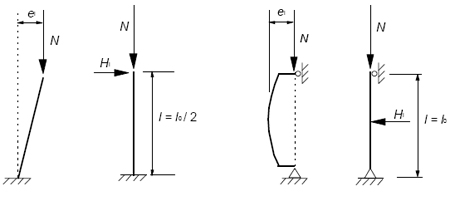
Figure 4. Éléments isolés soumis à une charge axiale excentrée ou à une charge transversale, exemples de l’effet des imperfections géométriques

 

3 Prise en compte des imperfections géométriques

Dans le cas d’éléments isolés, l représente la longueur réelle de l’élément et m est égal à 1. L’effet des imperfections (figure 4) peut être pris en compte de deux manières, au choix :
- comme une excentricité e_i donnée par e_i = θ_i.l₀/2 où l₀ est la longueur efficace (pour les éléments isostatiques),
- comme une charge transversale H_i, appliquée au point défavorable conduisant au moment maximal (pour les éléments isostatiques et hyperstatiques). Pour les éléments non contreventés on a H_i=θ_i.N, pour les éléments contreventés on a H_i=2θ_i.N où N est la charge axiale.

Dans le cas de voiles et de poteaux isolés dans des structures contreventées, il est toujours possible, pour simplifier, d’adopter e_i=L₀/400, ce qui correspond à α_h=1.

Système de contreventement           Plancher                      Diaphragme de                                         de contreventement      toiture

Figure 5. Exemples de l’effet des imperfections géométriques

 
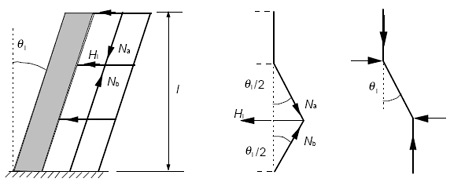
Dans le cas de système de contreventement, l représente la hauteur du bâtiment et m le nombre d’éléments verticaux transmettant la force horizontale appliquée au système de contreventement. L’effet des imperfections (figure 5) peut être pris en compte par des charges transversales H_i à ajouter aux autres actions dans l’analyse : H_i=θ_i(N_b-N_a).

Dans le cas de plancher de contreventement transmettant les forces horizontales, l représente la hauteur de l’étage et m le nombre d’éléments verticaux dans l’étage transmettant la force horizontale totale appliquée au plancher. L’effet des imperfections (figure 10) peut être pris en compte par des charges transversales H_i à ajouter aux autres actions dans l’analyse : H_i=θ_i(N_b-N_a)/2.

Dans le cas de diaphragme de toiture transmettant les forces horizontales, l représente la hauteur de l’étage et m le nombre d’éléments verticaux dans l’étage transmettant la force horizontale totale appliquée au plancher. L’effet des imperfections (figure 5) peut être pris en compte par des charges transversales H_i à ajouter aux autres actions dans l’analyse : H_i=θ_i.N_a).

4 Effet du fluage

La prise en compte du fluage s’effectue en considérant les effets généraux du fluage (article [3.1.4] de l’EC2) tels que l’humidité ambiante, la dimension des éléments et la composition du béton.
En outre la durée d’application des charges est prise en compte au moyen d’un coefficient de fluage effectif φ_ef défini en sorte que, sous la charge de calcul, la déformation de fluage soit la même que celle que l’on obtiendrait sous charges quasi permanentes avec le coefficient de fluage de base φ.

φef = φ(∞,t₀) M_0Eqp/M_0Ed

où :
• φ(∞,t₀) est le coefficient de fluage final défini dans l’article [3.1.4] de l’EC2.
• M_0Eqp est le moment fléchissant du 1^er ordre sous la combinaison de charges quasi permanentes (ELS).
• M_0Ed le moment fléchissant du 1^er ordre sous la combinaison de charges de calcul (ELU).

Remarques
• Si le rapport des moments fléchissants varie le long de la structure, on peut le calculer dans la section de moment maximal, ou utiliser une valeur moyenne représentative.
• On peut négliger l’effet du fluage (c’est-à-dire prendre φ_ef = 0) si on a à la fois :
φ(∞,t₀) ≤ 2, λ≤75, M_0Ed/N_Ed≥ h (h hauteur de la section droite dans le plan de flexion sous l’effet du moment du 1^er ordre M_0Ed).
• Si les conditions permettant de s’affranchir des effets du 2^e ordre sont tout juste satisfaites, négliger en plus les effets dus au fluage peut être préjudiciable sauf si le ratio mécanique d’armatures ω (défini au paragraphe 1.5.2) est tel que : ω ≥ 0.25.