1 Modélisation d’une poutre en béton armé
1.1. Modélisation d’une poutre en béton armé de section rectangulaire soumise à de la flexion simple
|
|
|
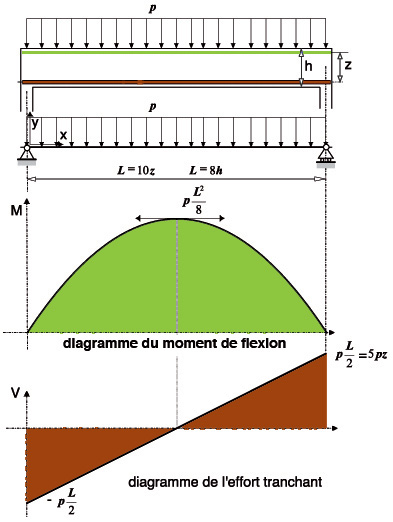
Figure 1 : Diagrammes de l’effort tranchant et du moment de flexion d’une poutre isostatique sollicitée par une charge uniformément répartie. |
La résistance des matériaux nous apprend que sous la seule action d’un moment de flexion positif, la poutre est sollicitée en compression dans la partie supérieure à l’axe neutre et en traction dans la partie inférieure.
La résistance du béton à la traction est faible, il ne peut reprendre, sans risque de rupture fragile, les contraintes de traction il est donc négligé dans les calculs.
Cet effort de traction doit être repris par un matériau compatible (adhérence mutuelle et coefficient de dilatation sensiblement le même pour les deux matériaux) et résistant en traction d’où la mise en place d’armatures longitudinales en acier (renvoi sur la barre rouge).
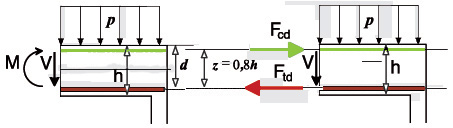
Ce premier modèle (= 2 membrures distantes de z, l’une travaillant en compression –renvoi sur la ligne bleue- l’autre en traction –renvoi sur la ligne rouge-) (Figure 2) permet de comprendre comment s’effectue la reprise du moment de flexion mais pas celle de l’effort tranchant.
|
|
|
Figure 2 : Première modélisation de la poutre en béton armé. |
1.2. Expérimentation
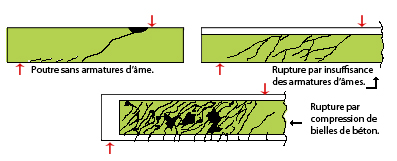
On distingue 3 types de ruptures :
- « Rupture pour les poutres sans armatures transversales »
- « Rupture par insuffisance d’armatures transversales »
- « Rupture par compression excessive des bielles de béton ».
|
|
Lors d'essais sur une poutre B.A. sans armatures d’âme, on constate l'apparition de fissures inclinées, celles-ci délimitent des prismes de béton inclinés à environ 45° (pour simplifier) sollicités en compression simple, ces prismes sont appelés bielles. (figure 4)
Ces fissures apparaissent d’abord au voisinage des appuis et se propagent ensuite vers la zone centrale de la travée.
|
|
|
Figure 3 : Fissuration de la poutre en béton armé. |
Montrons qu’il y a une corrélation entre l’intensité de l’effort tranchant et l’apparition et la propagation de ces fissures.
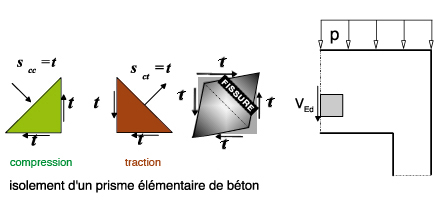
Isolons un cube élémentaire situé dans la zone tendue d’une poutre soumise à un effort tranchant. (figure 5)
Cet élément est situé proche de l’appui droit. L’étude des contraintes nous apprend que certaines de ses faces sont soumises uniquement qu’à des contraintes tangentes . On montre qu’une diagonale est comprimée tandis que l’autre est tendue. Si nous faisons varier l’intensité du chargement.
Lorsque la contrainte de traction (qui est aussi égale en intensité à la contrainte tangente) atteint la résistance de traction du béton , il se produit une fissure sensiblement inclinée à 45°.
|
|
|
Figure 4 : Isolement d’un prisme élémentaire de béton en zone tendue. |
1.3. Modélisation par une poutre treillis
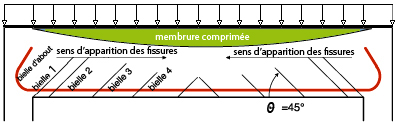
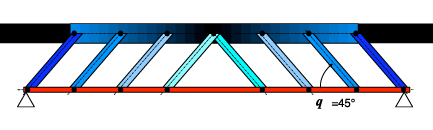
Si nous remplaçons les charges uniformément réparties par des forces ponctuelles régulièrement espacées, nous pouvons imaginer une modélisation tenant compte de la symétrie : les barres sont articulées au niveau de tous les nœuds.
|
|
|
Figure 5 : Treillis associé à la modélisation de la poutre en béton armé dépourvue d’armatures transversales. |
{La membrure comprimée comprend 6 barres, la membrure tendue comprend 7 barres, 8 diagonales soit 21 barres en tout : L = i-3b , le nombre d’inconnue total i obtenu en isolant tous les nœuds est égal à i = 57 d’où L = 57-3x21= - 6 donc L < 0, c’est un mécanisme instable}
remarque : on constate l’instabilité de cette structure : le treillis est constitué de 6 panneaux formant des parallélogrammes (lesquels sont déformables). Elle est à rejeter par le projeteur ou à transformer.
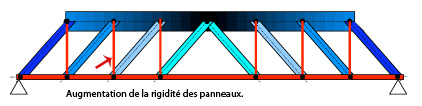
Pour rigidifier ces panneaux, il faut placer 6 diagonales qui sont ici verticales, on les appelle alors des montants).
Nous avons l’égalité 2n = b+3 (n = nombre de nœuds et b = nombre de barres) relation des systèmes matériels constitués de triangles qui est vérifiée, la structure est isostatique donc stable : L = 0. (figure 8)
|
|
|
Figure 6 : Treillis associé à la modélisation de la poutre en béton armé avec armatures transversales verticales. |
Ces montants représentent les armatures transversales en acier qu’il faut impérativement disposer dans la poutre pour assurer sa stabilité.
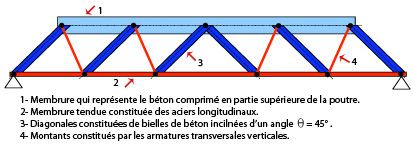
On modélise donc le fonctionnement mécanique d’une poutre en béton armé par un treillis que l’on nomme treillis de Ritter-Mörsch.
Les barres d’un treillis sont sollicitées uniquement à des efforts normaux soit de compression soit de traction. En béton armé, la barre comprimée est appelée bielle, la barre tendue tirant.
|
|
|
Figure 7 : Treillis associé à la modélisation de la poutre en béton armé avec armatures transversales inclinées. |
Les 2 membrures reprennent le moment de flexion.
Les diagonales et montants reprennent l’effort tranchant.
Ces commentaires apparaissent par fléchage ou clic sur les éléments.
On montrera, en étudiant le treillis, que les montants sont tendus et les diagonales (bielles de béton) comprimées.
Les montants tendus constituent les armatures d’âme ou transversales. Pour des raisons de facilité de montage des cages d’armatures elles sont verticales (90°) mais elles pourraient être inclinées, l’Eurocode permet une inclinaison de 45° à 90°.
Si nous plaçons des diagonales inclinées, nous avons aussi l’égalité 2n = b+3, la structure est isostatique donc stable. L= 0 (figure 9)