Modélisation de la géométrie de la structure
1. Classification des éléments en vue de l’analyse globale
Les éléments d’une structure de bâtiment sont classés, selon leur nature et leur fonction, en poutres, poteaux, dalles, voiles...
Une poutre est un élément dont la portée est supérieure ou égale à trois fois la hauteur totale de la section.
Une dalle est un élément dont la plus petite dimension dans son plan est supérieure ou égale à 5 fois son épaisseur totale.
Une dalle soumise principalement à des charges uniformément réparties peut être considérée comme porteuse dans une seule direction si l’une ou l’autre des conditions suivantes est remplie :
- elle présente deux bords libres (sans appuis) sensiblement parallèles,
- elle correspond à la partie centrale d’une dalle pratiquement rectangulaire appuyée sur 4 cotés et dont le rapport de la plus grande à la plus faible portée est supérieur à 2.
Un poteau est un élément dont le grand côté de la section transversale ne dépasse pas
4 fois le petit côté de celle-ci et dont la hauteur est au moins égale à 3 fois le grand côté. Lorsque ce n’est pas le cas, il convient de le considérer comme un voile.
Les dalles nervurées et les dalles à caissons peuvent ne pas être décomposées en éléments distincts pour les besoins de l’analyse, sous réserve que leur table de compression ou hourdis de compression rapporté, de même que leurs nervures transversales présentent une rigidité en torsion suffisante. On peut admettre que la rigidité en torsion est suffisante si :
- la distance entre nervures n’excède pas 1500 mm,
- la hauteur de la nervure sous la table de compression n’excède pas 4 fois sa largeur,
- l’épaisseur de la table de compression est supérieure ou égale à 1/10 de la distance libre entre nervures ou 50 mm si cette valeur est supérieure,
- la distance libre entre nervures transversales n’excède pas 10 fois l’épaisseur totale de la dalle.
2. Portée utilse des poutres et dalles dans les bâtiments
Il convient de calculer la portée utile leff d’un élément de la manière suivante :
leff = ln + a1 + a2
où ln est la distance libre entre nus des appuis et où les valeurs de a1 et a2 à chaque extrémité de la travée sont déterminées en fonction des conditions d’appui sur les figures 1 à 5.
Généralement leff correspond à la portée entraxe d’appuis de l’élément.
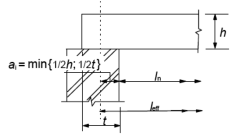 |
| Figure 1. Éléments isostatiques, portée utile leff |
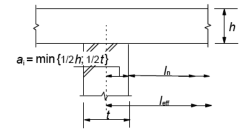 |
| Figure 2. Éléments continus, portée utile leff |
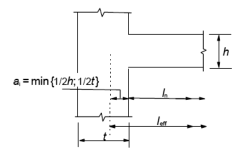 |
| Figure 3. Appuis considérés comme des encastrements parfaits, portée utile leff |
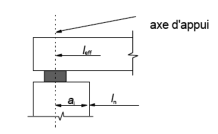 |
| Figure 4. Présence d’un appareil d’appui, portée utile leff |
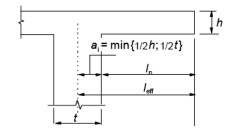 |
| Figure 5. Console, portée utile leff |
3. Largeur participante des tables de compression
L’épaisseur minimale de la table de compression peut être ramenée de 50 mm à 40 mm lorsque des entrevous permanents sont disposés entre les nervures. Pour l’analyse structurale, dans les cas où une grande précision n’est pas requise, on peut admettre une largeur constante sur toute la longueur de la travée. Il convient alors d’adopter la valeur applicable en travée.
Dans le cas des poutres en Té, il convient d’établir la largeur participante de la table de compression en fonction de la distance l0 entre points de moment nul, telle qu’indiquée par la figure 6. Il convient de limiter le rapport de deux portées adjacentes à des valeurs comprises entre 2/3 et 3/2 (2 /3<l1/l2<3/2). Pour la longueur l3 de la console, il convient de ne pas dépasser la moitié de la portée de la travée adjacente (l3<l2/2).
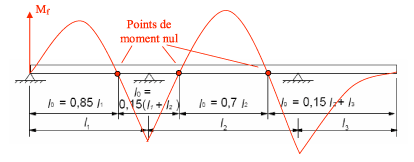 |
| Figure 6. Définition de l0 pour le calcul de la largeur participante de la table de compression |
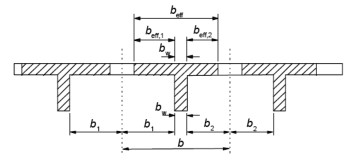 |
| Figure 7. Paramètres déterminant la largeur participante |
4. Modélisation mécanique spécifique aux dalles et poutres continues
Les dalles et poutres continues peuvent généralement être analysées en considérant que les appuis ne créent pas de gêne à la rotation.
Lorsqu’une poutre ou une dalle forme un ensemble monolithique avec ses appuis, il convient de prendre comme moment déterminant de calcul le moment au nu de l’appui (ce moment ne doit pas être inférieur à 0,65 fois le moment d’encastrement).
Lorsqu’une dalle ou une poutre est continue au droit d’un appui supposé ne pas créer de gêne à la rotation (au droit d’un voile par exemple), le moment de calcul sur appuis, déterminé pour une portée égale à l’entraxe des appuis, peut être minoré (figure 8) d’une valeur ΔMEd = FEd,sup.t/8
FEd,sup est la valeur de calcul de la réaction d’appui
t est la profondeur de l’appui (lorsque des appareils d’appuis sont utilisés, t est la largeur de l’appareil d’appuis).
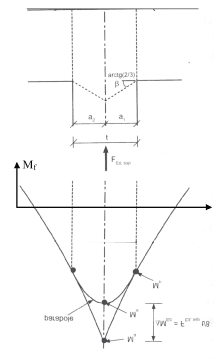 |
| Figure 8 : Ecretâge du moment sur appui |
5. Prise en compte des imperfections géométriques d’éléments de la structure
Aux états limites ultimes, l’analyse des éléments et des structures doit tenir compte des effets défavorables des imperfections géométriques éventuelles de la structure ainsi que des écarts dans la position des charges. La prise en compte des ces imperfections s’applique aux éléments soumis à une compression axiale et aux structures de bâtiment soumises à des charges verticales.
Les imperfections peuvent être représentées par une inclinaison θi :
θi = θ0.αh.αm
où
θ0 est la valeur de base : θ0 = 1/200
αh est un coefficient de réduction relatif à la longueur ou la hauteur : αh = 2/l0,5
αm est un coefficient de réduction relatif au nombre d’éléments : αm = [0,5(1+1/m)]0,5
l est une longueur ou une hauteur exprimée en mètres
m est le nombre d’éléments verticaux contribuant à l’effet total
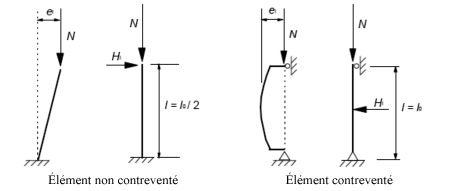 |
| Figure 9. Éléments isolés soumis à une charge axiale excentrée ou à une charge transversale, exemples de l’effet des imperfections géométriques |
Dans le cas d’éléments isolés, l représente la longueur réelle de l’élément et m est égal à 1. L’effet des imperfections (figure 9) peut être pris en compte de deux manières, au choix :
comme une excentricité ei donnée par ei = θi.l0/2 où l0 est la longueur efficace (pour les éléments isostatiques),
comme une charge transversale Hi, appliquée au point défavorable conduisant au moment maximal (pour les éléments isostatiques et hyperstatiques). Pour les éléments non contreventés on a Hi=θi.N, pour les éléments contreventés on a Hi=2θi.N où N est la charge axiale.
Dans le cas de voiles et de poteaux isolés dans des structures contreventées, il est toujours possible, pour simplifier, d’adopter ei=L0/400, ce qui correspond à αh=1.
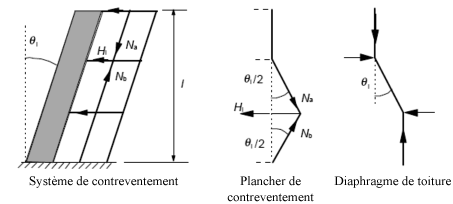 |
| Figure 10. Exemples de l’effet des imperfections géométriques |
Dans le cas de système de contreventement, l représente la hauteur du bâtiment et m le nombre d’éléments verticaux transmettant la force horizontale appliquée au système de contreventement. L’effet des imperfections (figure 10) peut être pris en compte par des charges transversales Hi à ajouter aux autres actions dans l’analyse : Hi=θi(Nb-Na).
Dans le cas de plancher de contreventement transmettant les forces horizontales, l représente la hauteur de l’étage et m le nombre d’éléments verticaux dans l’étage transmettant la force horizontale totale appliquée au plancher. L’effet des imperfections (figure 10) peut être pris en compte par des charges transversales Hi à ajouter aux autres actions dans l’analyse : Hi=θi(Nb-Na)/2.
Dans le cas de diaphragme de toiture transmettant les forces horizontales,
l représente la hauteur de l’étage et m le nombre d’éléments verticaux dans l’étage transmettant la force horizontale totale appliquée au plancher. L’effet des imperfections (figure 10) peut être pris en compte par des charges transversales Hi à ajouter aux autres actions dans l’analyse : Hi=θi.Na).