Accueil/Cours/Matériaux /Modélisation du béton

PARAMETRES CARACTERISTIQUES ET LOI DE CALCUL DU BETON

1 Comportement en compression

Modules d’élasticité

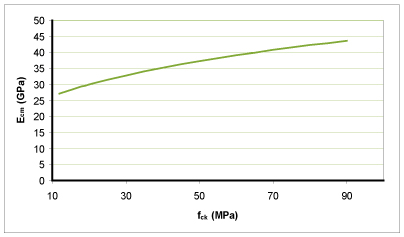
Le module d'élasticité du béton adopté conventionnellement pour les calculs (sauf pour les effets différés), E_cm est un module sécant mesuré entre σ_c = 0 et 0,4 f_cm. Il peut être estimé à l'aide de la relation suivante :
E_cm (GPa) = 22.[(f_cm)/10]^0,3 avec f_cm en MPa. La figure 1 donne l'évolution du module avec la résistance. On remarque qu'il augmente moins vite que celle-ci. Cette relation n'est qu'indicative. En effet, le module du béton dépend de la composition de celui-ci et, notamment, de la nature des granulats. Pour les bétons auto plaçants (BAP), la quantité de pâte plus importante peut entraîner un module plus faible. L'Eurocode Béton indique que le module peut être plus faible de 10 à 30% pour des calcaires et des grès et plus fort de 20% pour des basaltes. Le module doit donc être déterminé de manière explicite si la structure est sensible à sa valeur.

Figure 1 : évolution du module avec la résistance (relation moyenne de l'EC2)

Relations contrainte-déformation

Hors problème d'instabilités, ce comportement est pris en compte de manière simplifiée dans l'Eurocode Béton par l'expression suivante :

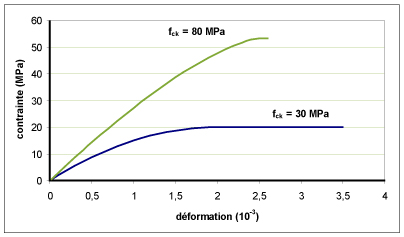
`sigma_c =f_(cd)[1-(1-epsi_c/epsi_(c2))^n] pour 0<=epsi_c <=epsi_(c2) et sigma_c=f_(cd) pour epsi_(c2) <=epsi_c<=epsi_(cu2) `

les valeurs de n, ε_c2 et ε_cu2 étant définis dans le tableau 1. f_cd est la résistance de calcul en compression. Elle se déduit de la résistance caractéristique en la divisant par le coefficient partiel de sécurité γ_c et par un coefficient α_cc (tenant compte des effets à long terme sur la résistance en compression et des effets défavorables résultant de la manière dont la charge est appliquée ; sa valeur recommandée est égale à 1). ε_c2 et ε_cu2 sont respectivement la déformation du béton lorsque la contrainte atteint f_cd et la déformation maximale du béton. La figure 2 présente deux exemples de la loi de comportement réglementaire. La partie plastique de la loi de comportement réglementaire rend compte de manière simplifiée du comportement radoucissant du béton. Cette partie est moins importante pour les bétons à très hautes performances car ils ont une perte de raideur très marquée dans la partie radoucissante.

f_ckMPa	≤ 50	60	70	80	90
n	2	1,6	1,45	1,4	1,4
ε_c2 (⁰/₀₀)	2	2,2	2,4	2,5	2,6
ε_c2 (⁰/₀₀)	3,5	2,9	2,7	2,6	2,6

Tableau 1 : extrait du tableau 3.1 de la norme NF EN 1992 -1.3. On notera que lorsque la résistance augmente le comportement devient plus linéaire (n se rapproche de 1) et la déformation à rupture diminue.

Figure 2 : exemples de lois de comportement de calcul pour f_ck= 30 MPa et f_ck = 80 MPa avec γ_c = 1,5 et α_cc =1.

Nota : on retrouve bien le diagramme parabole-rectangle pour les bétons de résistance ≤ 50 MPa. Pour l'analyse structurale non-linéaire (flambement) l'Eurocode Béton propose une relation contrainte-déformation comportant une partie radoucissante (expression 3.14 de l'Eurocode Béton). Enfin, l'Eurocode Béton autorise l'emploi d'autres relations pourvu qu'elles représentent correctement le comportement du béton (par exemple, pour le béton confiné, l'EC2 propose une relation prenant en compte l'effet du confinement sur le comportement).

2 Comportement en traction

La résistance en traction moyenne du béton f_ctm est estimée dans l'Eurocode Béton par les relations suivantes :
f_ctm = 0,30 f_ck^(2/3) lorsque f_ck ≤ 50 MPa
f_ctm = 2,12 ln(1+(f_cm)/10) lorsque f_ck > 50 MPa
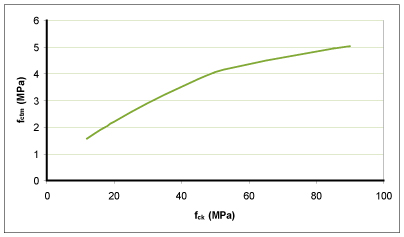
La figure 3 présente l'évolution de f_ctm en fonction de f_ck. On constate que la valeur de f_ctm reste faible même pour les bétons à hautes performances. De fait, la résistance en traction est peu utilisée directement dans le dimensionnement.

Figure 3 : évolution de la résistance en traction f_ctmen fonction de f_ck

3 Comportement différé du béton : retrait et fluage

Lorsque le béton n'est pas chargé il se déforme spontanément : c'est le retrait. La déformation totale de retrait ε_cs est la somme de deux contributions :
- le retrait endogène ε_ca qui est la conséquence de l'autodessiccation du béton (l'humidité interne du béton diminue lorsque le ciment consomme l'eau pour s'hydrater). C'est une fonction linéaire de la résistance en compression (car pour obtenir une résistance élevée il faut un rapport E/C faible et on a donc une autodessiccation importante) ;
- le retrait de dessiccation ε_cdqui est la conséquence du séchage naturel du béton. Il dépend de la taille des pièces.

La déformation de fluage ε_cc(∞, t₀) sous une contrainte de compression σ_c est égale à :

φ (∞, t₀).( σ_c/E_c)

où E_c est le module tangent (égal à 1,05 E_cm) et φ est le coefficient de fluage. L'Eurocode Béton donne une méthode simplifiée de calcul de φ(∞, t₀). L'annexe B donne une méthode plus complète permettant d'estimer φ (t, t₀) ainsi que l'évolution du retrait (voir également l'annexe B de l'EC2-2).

Le calcul des déformation différées fait intervenir le type de ciment. L'Eurocode Béton classe les ciments en 3 catégories (cf. tableau 3)

Classes EC2

Classes de résistance des ciments

selon la norme NF EN 197-1

42,5 R

32,5 R

52,5 N
52,5 R

42,5 N

Tableau 2 : classes de ciment selon l'EC2 et équivalence avec les classes de la norme ciment NF EN 197-1

L'Eurocode Béton fournit également des formules d'évolution des résistances en traction et en compression au cours du temps. Ces formules dépendent de la classe du ciment (tableau 2). En pratique, cependant, l'essentiel du dimensionnement se fait à partir de f_ck, dont on déduit les différentes caractéristiques de calcul. Les structures dont la déformabilité est critique (grands ouvrages en béton précontraint, immeubles de très grande hauteur par exemple) peuvent cependant requérir une identification plus précise des caractéristiques en cause (module d'élasticité, coefficients de retrait-fluage).