METHODE GENERALE
Dans le cas où l’on doit tenir compte des effets du 2e ordre, l’EC2 propose une méthode générale (article 5.8.6).
• La loi de comportement du béton est celle définie par l’expression de l’article 3.1.5 de l’EC2 en remplaçant fcm par fcd et Ecm par Ecd (on prend les valeurs de calcul et
Ecm = Ecd/YcE, la valeur de YcE recommandée par l’EC2 et reprise dans l’annexe nationale est YcE=1.2.
• Pour les aciers, c’est la loi donnée dans l’article 3.2.7 qui sert de base aux calculs en considérant au choix soit le diagramme avec palier soit le diagramme avec droite inclinée.
• La prise en considération du fluage du béton se fait en multipliant les valeurs des déformations relatives du béton par (1+φef).
• L’effet favorable du béton tendu est souvent négligé pour simplifier les calculs.
En outre il est fait l’hypothèse d’une déformée sinusoïdale sur la hauteur du poteau.
La méthode de calcul est dérivée de la méthode de Faessel dont la démarche est la suivante :
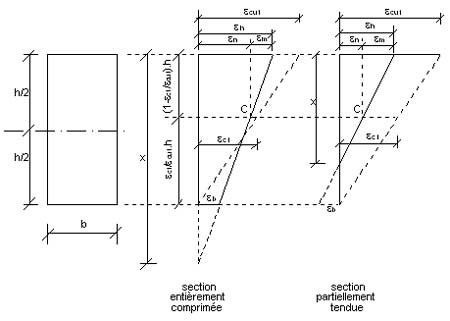
On considère une droite de déformation de la section béton caractérisée par un couple (εm,εn) (cf. figure 1).
|
|
| Figure 1 : Diagramme des déformations de la section rectangulaire (d’après [1]) |
Pour tout couple, on peut calculer les sollicitations résistantes NRd et MRd par la relation : `e_i + M_(Ed)/N_(Ed) +e_2 - M_(Rd)/N_(Rd) = 0`
, qui traduit l’équilibre : excentricité agissante=excentricité résistante
avec :
ei excentricité due aux imperfections géométriques prise à L0/400 (article 5.2 de l’EC2)
eo excentricité extérieure du 1er ordre = MRd/NRd
e1 excentricité totale du 1er ordre = eo+ei
e2 excentricité du 2e ordre = `(epsi_h - epsi_b)/h (L_o/pi)^2`
h épaisseur du poteau dans le sens du flambement
HR humidité relative en %
Lo longueur de flambement
MEd moment agissant en ELU
NEd effort normal agissant en ELU
MRd moment résistant de la section critique
NRd effort normal résistant de la section critique
r rayon de courbure de la section critique
εh déformation en fibre la plus comprimée
εb déformation en fibre tendue ou la moins comprimée
εc1 déformation du béton sous contrainte maximale fck
εcu1 déformation maximale du béton à la rupture
φef coefficient de fluage effectif
Une représentation graphique permet alors d’en déduire MRD et NRD.
Remarque : Il est possible d’utiliser des formules simplifiées de détermination de la force portante NRD dans le cas où les conditions suivantes sont remplies.
- poteau de bâtiment bi-articulé sous charges centrées
- élancement ≤ 120
- 20 ≤ fck ≤ 50 MPa
- épaisseur dans le sens du flambement : h ≥ 0,15 m
- distance d’ des aciers à la paroi la plus proche ≤ Min[0,30 h ; 100 mm]
- armatures symétriques : As/2 sur chaque face
- chargement à au moins 28 jours
- ciments normaux (N) ou rapide (R)
- taux d’humidité relative : 40 ≤ RH ≤ 100 %
et ceci sous la forme générique :
|
Section rectangulaire `N_(Rd) = k_hk_s.alpha.``[b.h.f_(cd)+A_s.f_(yd)]` `alpha = 0.86/(1+(lambda/62)^2)` si `lambda <= 60` `alpha = (32/lambda)^(1,3)` si `60` `k_h = (0,75+0,5h).(1-6rhodelta)` pour `h<50` sinon `k_h = 1` `k_s = 1,6 - 0,6 f_(yk)/(500)` pour `f_(yk) > 500` et `lambda > 40` sinon `k_s = 1` |
|
1. Section circulaire `N_(Rd) = k_n.k_s.alpha.``[(piD^2)/4.f_(cd)+A_s.f_(yd)]` `alpha = (0,84)/(1+(pi/52)^2` si `lambda <=60` `alpha = (27/lambda)^(1,24)` si `60` `k_h=(0.7+0.5D).(1-8rhodelta)` pour `D<60` sinon `k_h=1` `k_s = 1,6-0,65 f_(yk)/500` pour `f_(yk)>500` et `lambda>30` sinon `k_s=1` |
b = largeur du poteau rectangulaire
D = diamètre de la section circulaire
d’ = enrobage : distance de l’axe de l’acier à la paroi la plus proche
h = épaisseur du poteau rectangulaire dans le sens du flambement
Lo = longueur de flambement
fcd=fck/1,5 ; fyd=fyk/1,15
As = section totale des aciers situés à la distance d’ des parois, disposés en deux lits pour une section rectangulaire ou en six barres pour une section circulaire